快速排序概要

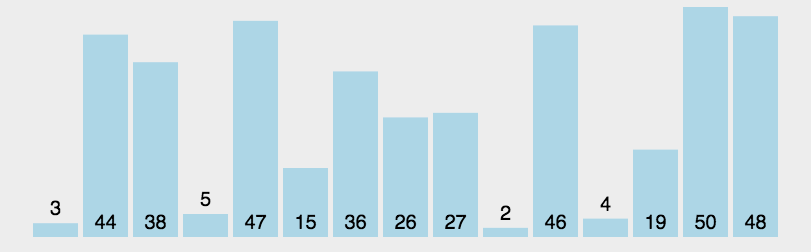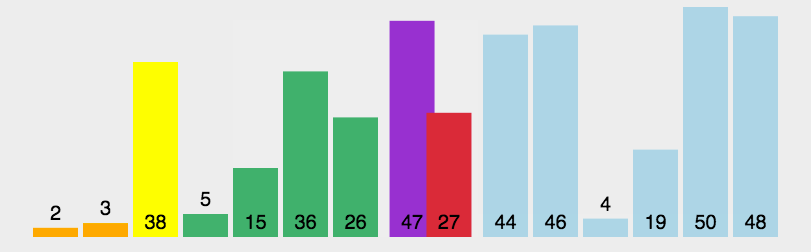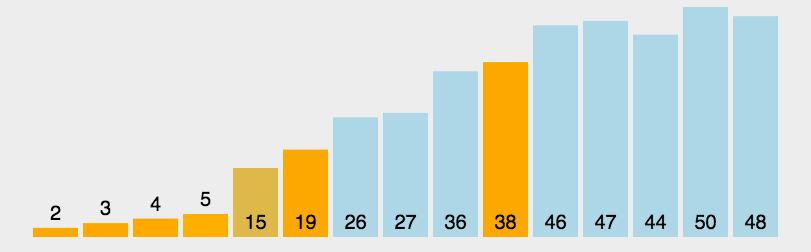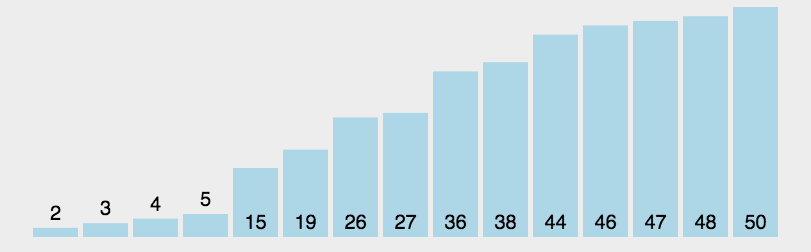
快排的三个步骤：

• 选择基准：在待排序列中，按照某种方式挑出一个元素，作为 “基准”（pivot）。
• 分割操作：以该基准在序列中的实际位置，把序列分成两个子序列。此时，在基准左边的元素都比该基准小，在基准右边的元素都比基准大。
• 递归地对两个序列进行快速排序，直到序列为空或者只有一个元素。

其实快排实现的核心思想就是分治和递归，接下来用大白话解释下快排的原理，用词和说明可能不是那么正确，但是能够先听懂它的实现，我觉得这更重要。

我们假设这样杂乱无序不重复的数组[21, 5, 44, 63, 3]，设定他的基准pivot为第一位Array[0]，则pivot就是21，当然不一定都是第一位，并且low指针指向最左边，high指针指向最后边。

当low指针指向的值大于pivot就赋值给high指针，若当前指向的值不大于pivot，则一直向右移动，直到两个指针重合或者找到比pivot大的值。

high指针则反之，一直找寻比pivot小的值，找到则赋值给low指针，否则一直向左移动，直到两个指针重合或者找到比pivot小的值。

快排原理解释

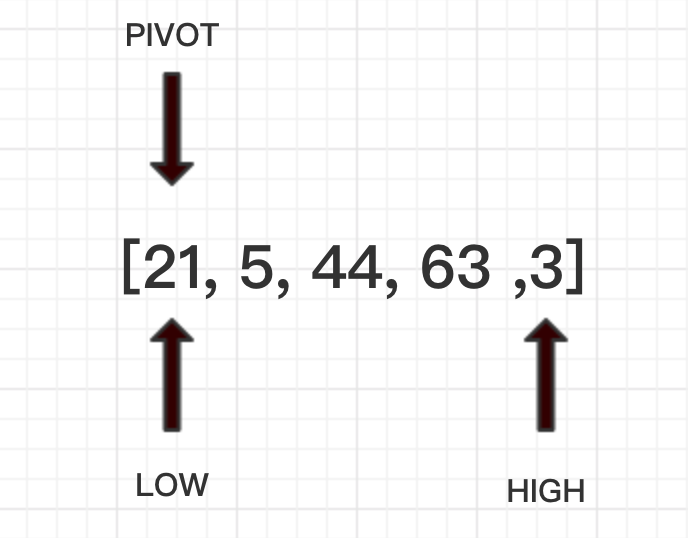
high指针先于low指针比较和移动，high指针所指向的value是3，比pivot小，则赋值给low指针所指向的21，并且high指针不动。

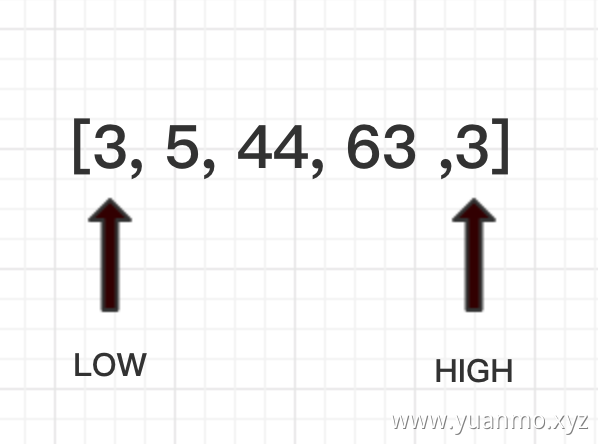
这时，轮到low指针向右移动了。

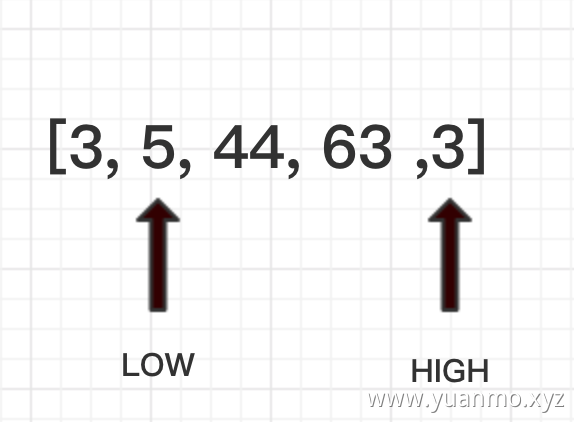
此时low指针向右移动发现比pivot小，则继续向右移动。

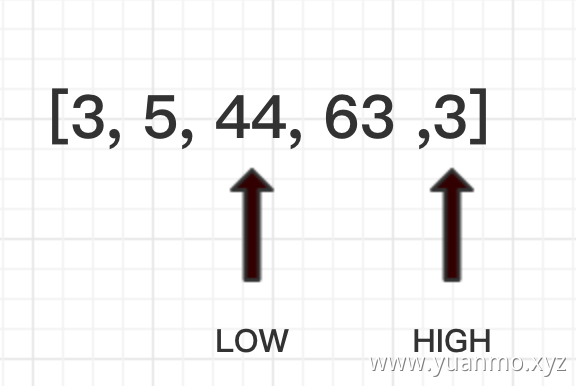
这时候lei了，low指针指向的44比pivot大，辣么就赋值给high指针指向的3，并且low指针保持不动。

high指针向左移动。

发现比pivot大，这继续向左移动。

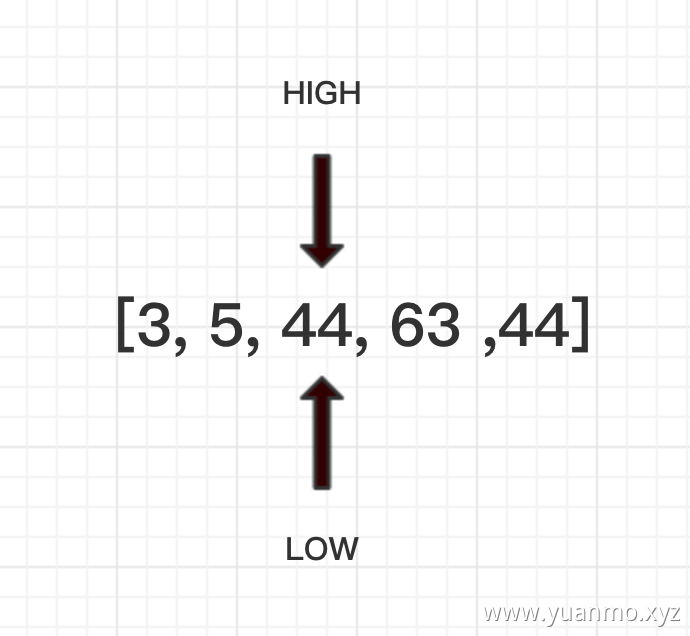
当两指针重合的时候，此时指向的44将会被基准值改写。

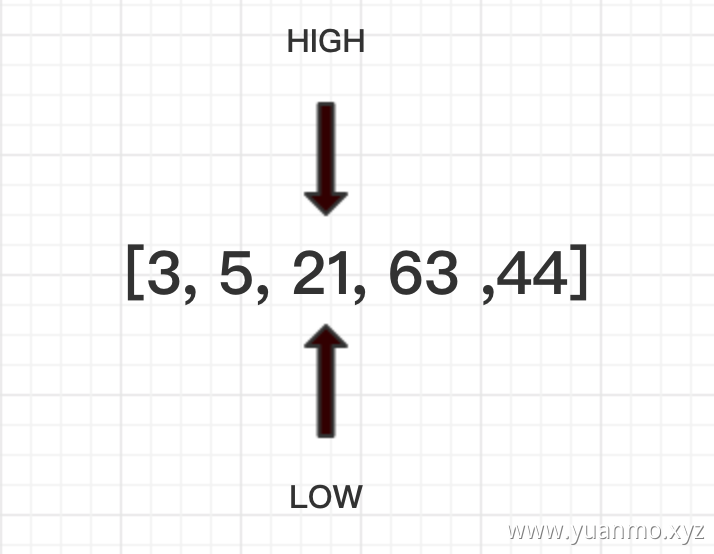
这时候一轮分治就OJBK了。可以清楚地看到（好像这个例子不是很清楚的看到，果然是size太短了吗），在基准值的左边数组大小都是小于基准值的，而右边数组都是大于基准值。这个时候就体现了快排的分治思想，相当于从基准中切一刀，左边的数组单独去排序，右边的数组单独去排序。这时候就变成了[3, 5]和[63, 44]继续递归快速排序，所以说快排实现的核心思想就是分治和递归。

Java代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53

package sort;

import java.util.Arrays;
import java.util.Timer;

/**
 * @author Matthew Han
 * @description
 * @date 2021/4/21 17:06
 * @since 1.0.0
 **/
public class QuickSort<T extends Comparable<T>> implements ISort<T> {
    /**
     * 快速排序
     *
     * @param arr
     */
    @Override
    public void sort(T[] arr) {
        quickSort(arr, 0, arr.length - 1);
        System.out.println("arr = " + Arrays.toString(arr));
    }

    public void quickSort(T[] arr, int left, int right) {
        if (left > right) {
            return;
        }
        int i = left;
        int j = right;
        T pivot = arr[i];
        while (i < j) {
            while (i < j && arr[j].compareTo(pivot) >= 0) {
                j--;
            }
            if (i < j && arr[j].compareTo(pivot) < 0) {
                arr[i] = arr[j];
                i++;
            }
            while (i < j && arr[i].compareTo(pivot) < 1) {
                i++;
            }
            if (i < j && arr[i].compareTo(pivot) > 0) {
                arr[j] = arr[i];
                j--;
            }
        }
        if (i == j) {
            arr[i] = pivot;
        }
        quickSort(arr, left, i - 1);
        quickSort(arr, i + 1, right);
    }
}

要注意每次要判断i和k的大小，因为数组size是多少就会有多少次基准数归位，会不断地拆分成两对数组，最后变成2位，1位。

快排的一些知识点和算法复杂度

• 选取基准最怕的就是选到了最大值或者最小值，这样一轮就是只是把基准数移到了最边上。
• 从概率学上来说，基准数选不选择第一个，还是中间随机抽取一个对是否会选取到最大值或最小值都是没有任何影响的。但是存在数列完全逆序的情况，从中间选取基准数可以有效避免这种情况发生，若还是选择数列最左位当做基准数的话，就会变成最糟糕的情况，时间复杂度就会变成O（n^2）。
• 所以快速排序的平均时间复杂度是 O（nlogn），最坏情况下的时间复杂度是 O（n^2）。

• ← Previous Post
• Next Post →